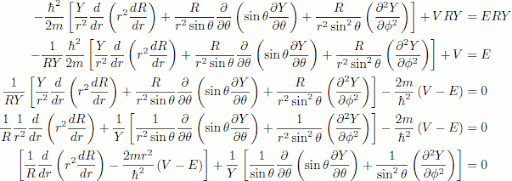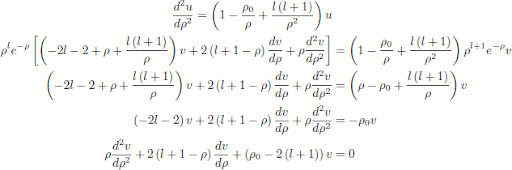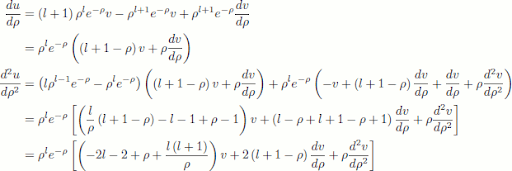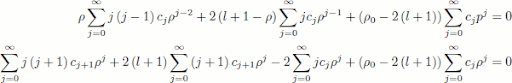When I was studying for my quantum physics exam on Wednesday before last, this struck me as very elegant, albeit rather long and difficult. I had worked through it by hand, as I like doing that when I study as just reading doesn't make things sink into my brain, so I thought I'd put these notes up here, for anyone who's interested (plus, I like playing in LaTeX).
Think of when this was first done, Schrödinger was trying to see if his equation would fit in with observed phenomena, things known at the time, so he initially solved it for the hydrogen atom, which was known. Not any of these infinite square wells, harmonic oscillators, etc. you start with nowadays, as only recently have we become able to observed the effects of these.
So prepare yourself for a whole lot of maths, with a little physics woven in between.
Time-independent Schrödinger equation in spherical coordinates
So we start off with the time-independent Schrödinger equation (in 3D):
−ℏ22m∇2ψ+Vψ=Eψ
In spherical coordinates, the Laplacian becomes (according to
wikipedia (therefore true) and other places):
∇2=1r2∂∂r(r2∂∂r)+1r2sinθ∂∂θ(sinθ∂∂θ)+1r2sin2θ(∂2∂ϕ2)
Thus the time-independent Schrödinger equation becomes:
First, look for separable solutions of the form
ψ(r,θ,ϕ)=R(r)Y(θ,ϕ), which gives:
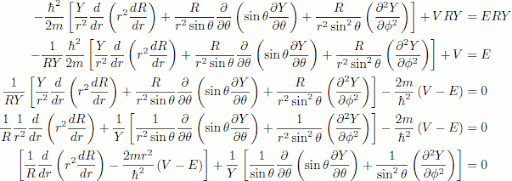
Now, if the potential,
V only depends on
r then the first of these square brackets only depends on
r and the second only depends on
θ and
ϕ. Thus they must both be equal to a constant, lets call this
l(l+1) (because I like being difficult), so:
1Rddr(r2dRdr)−2mr2ℏ2(V−E)=l(l+1)1Y[1sinθ∂∂θ(sinθ∂Y∂θ)+1sin2θ(∂2Y∂ϕ2)]=−l(l+1)
The Radial Equation
The first of the above two equations can be simplified by letting
u(r)=rR(r). Now:
dudr=R+rdRdrand sodRdr=dudr−Rr=dudr−urr=rdudr−ur2thusddr(r2dRdr)=ddr(rdudr−u)=dudr+rd2udr2−dudr=rd2udr2
Now subbing into the earlier equation:
1Rddr(r2dRdr)−2mr2ℏ2(V−E)=l(l+1)rurd2udr2−2mr2ℏ2(V−E)=l(l+1)d2udr2−2mℏ2u(V−E)=l(l+1)ur2ℏ22md2udr2−u(V−E)=ℏ22ml(l+1)ur2−ℏ22md2udr2+(V+ℏ22ml(l+1)r2)u=Eu
That looks pretty familiar, doesn't it?
Hydrogen Atom
Now that the basis is there, we can actually start looking at stuff specific to the hydrogen atom. Firstly, the potential energy function is Coulomb's law:
V(r)=−e24πε01r
Subbing this into the radial equation derived above gives:
−ℏ22md2udr2+(−e24πε01r+ℏ22ml(l+1)r2)u=Eu
Now let
k=√−2mEh, which is, of course, real as we're looking at the bound states, so
E<0. Manipulating the radial equation gives:
−ℏ22mEd2udr2+(−e24πε01r1E+ℏ22mEl(l+1)r2)u=u1k2d2udr2+(−e24πε01r1Ek2k2−1k2l(l+1)r2)u=u1k2d2udr2+(e24πε01r2mℏ21k2−1k2l(l+1)r2)u=u
1k2d2udr2=(1−me22πε0ℏ21r1k2−1k2l(l+1)r2)u
This isn't looking very good, so lets try another substitution,
ρ=kr and
ρ0=me22πε0ℏ2k. With these,
d2udr2=d2udρ2d2ρdr2=d2udρ21k2, so we get:
d2udρ2=(1−ρ0ρ+l(l+1)ρ2)u
This looks a whole lot simpler, but is still not easy to solve. We'll try breaking off the behaviour of
r and thus
ρ tends to 0 and
+∞.
lim
with solution:
u \left( \rho \right) = A e^{-\rho} + B e^{\rho}
and (assuming
l \neq 0):
\lim_{\rho \to 0} \frac{d^2u}{d\rho^2} = \frac{l \left( l + 1 \right)}{\rho^2} u
Unlike the previous equation, the solution to this isn't well known (at least to me), but can be easily solved by the power series method. Propose a solution,
u = \sum_{n=-\infty}^{+\infty} a_n \rho^n . This has derivatives:
\frac{du}{d\rho} = \sum_{n=-\infty}^{+\infty} n a_n \rho^{n-1} \quad \mathrm{and} \quad \frac{d^2u}{d\rho^2} = \sum_{n=-\infty}^{+\infty} n \left( n - 1 \right) a_n \rho^{n-2}
Subbing these into the differential equation gives:
\begin{aligned} \sum_{n=-\infty}^{+\infty} n \left( n - 1 \right) a_n \rho^{n-2} &= \frac{l \left( l + 1 \right)}{\rho^2} \sum_{n=-\infty}^{+\infty} a_n \rho^n \\ \sum_{n=-\infty}^{+\infty} n \left( n - 1 \right) a_n \rho^{n-2} &= l \left( l + 1 \right) \sum_{n=-\infty}^{+\infty} a_n \rho^{n-2}\end{aligned}
Which is only true when
n \left( n - 1 \right) = l \left( l + 1 \right) ,
n = l + 1, -l . So all other
a_n must be zero, giving the solution:
\begin{aligned} u \left( \rho \right) &= a_{l+1} \rho^{l + 1} + a_{-l} \rho^{-l} \\ &= C \rho^{l + 1} + D \rho^{-l}\end{aligned}
Now if you're anything like me, you'll want to double check this, so lets do that now:
\begin{aligned} \frac{du}{d\rho} &= \left(l+1\right) C \rho^l - l D \rho^{-l-1}\\ \frac{d^2u}{d\rho^2} &= l \left(l+1\right) C \rho^{l-1} - \left(-l-1\right) l D \rho^{-l-2}\\ &= l \left(l+1\right) \left( C \rho^{l-1} + D \rho^{-l-2} \right)\\ &= \frac{l \left(l+1\right)}{\rho^2} u\end{aligned}
So yep, this is a solution (well, family of solutions). However, as
r and correspondingly
\rho tends to zero, the second term tends to infinity, so
D must be zero. So now combining these, we get:
u \left( \rho \right) = \rho^{l+1} e^{-\rho} v \left( \rho \right)
In the hope that
v\left(\rho\right) will be easier to solve than
u\left(\rho\right). Now we want to get the radial equation in terms of
v rather than
u. So first we'll find its derivatives:
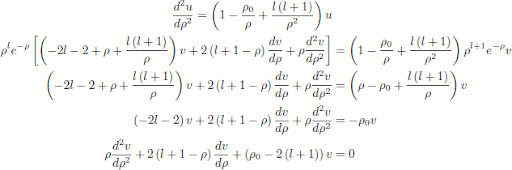
And now subbing this into the radial equation:
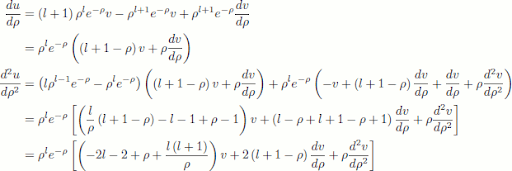
Which isn't all too bad really, but is still not easy to solve. Again, lets go down the power series route, proposing a solution of the form
v \left( \rho \right) = \sum_{j=0}^{\infty} c_j p^j. The derivatives are:
\frac{dv}{d\rho} = \sum_{j=0}^{\infty} j c_j \rho^{j-1} \quad \mathrm{and} \quad \frac{d^2v}{d\rho^2} = \sum_{j=0}^{\infty} j \left( j - 1 \right) c_j \rho^{j-2}
Subbing these in gives:
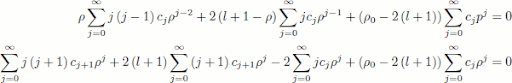
Now, by equating the coefficients of
\rho^j, we get:
\begin{aligned} j \left( j + 1 \right) c_{j+1} + 2 \left( l + 1 \right) \left( j + 1 \right) c_{j+1} - 2 j c_j + \left(\rho_0 - 2 \left(l+1\right) \right) c_j &= 0 \\ \left( j + 1 \right) \left[ j + 2 \left( l + 1 \right) \right] c_{j+1} - \left[ 2j - \rho_0 + 2 \left( l + 1 \right) \right] c_j &= 0\end{aligned}
Which gives the recurrence relation:
c_{j+1} = \frac{ 2 \left( j + l + 1 \right) - \rho_0}{\left( j+1 \right) \left( j + 2l + 2 \right)} c_j
But at large
j (and
\rho),
c_{j+1} = \frac{2j}{j \left( j+1 \right)} c_j = \frac{2}{j+1} c_j . Suppose this were the actual solution, then:
c_j = \frac{2}{j} c_{j-1} = \frac{2}{j} \frac{2}{j-1} c_{j-2} = \cdots = \frac{2^j}{j!} c_0
And then:
v \left( \rho \right) = c_0 \sum_{j=0}^{\infty} \frac{2^j}{j!} p^j = c_0 e^{2\rho}
By the power series definition of the exponential function. Hence:
\begin{aligned} u \left( \rho \right) &= \rho^{l+1} e^{-\rho} v \left( \rho \right) \\ &= c_0 \rho^{l+1} e^\rho\end{aligned}
Which goes to infinity as
\rho (and thus
r) tends to infinity, which is not good. These are mathematical solutions to the equation, but are not normalisable so aren't physical solutions. Thus the series has to terminate somewhere, i.e. there must be some
j_{max} such that
c_{j_{max} + 1} = 0 (and all later terms will also be zero be the recurrence relation). Thus, by going back to the recurrence relation:
c_{j_{max}+1} = \frac{ 2 \left( j_{max} + l + 1 \right) - \rho_0}{\left( j_{max}+1 \right) \left( j_{max} + 2l + 2 \right)} c_{j_{max}} = 0
2 \left( j_{max} + l + 1 \right) - \rho_0 = 0
Now, lets define the principle (my textbook called this principal, but surely that's incorrect) quantum number,
n, to be
\left(j_{max} + l + 1\right) and thus
\rho_0 = 2n. Now going way back, remember
k = \frac{\sqrt{-2mE}}{\hbar},
\rho = kr and
\rho_0 = \frac{me^2}{2 \pi \varepsilon_0 \hbar^2 k}. So
\begin{aligned} 2n &= \frac{me^2}{2 \pi \varepsilon_0 \hbar^2 k} \\ \frac{\sqrt{-2mE_n}}{\hbar} &= \frac{me^2}{4 \pi \varepsilon_0 \hbar^2 n} \\ -2mE_n &= \frac{m^2e^4}{16 \pi^2 \varepsilon_0^2 n^2 \hbar^2} \\ E_n &= - \frac{me^4}{32 \pi^2 \varepsilon_0^2 n^2 \hbar^2} \\ &= \frac{E_1}{n^2}\end{aligned}
These are the
allowed energies of the electron, which were known before the Schrödinger equation was developed. Though it was formulated by Niels Bohr somewhat arbitrarily. Also,
k can be nicely expressed in terms of the
Bohr radius,
a_0 = \frac{4 \pi \varepsilon_0 \hbar^2}{me^2} = 0.529 \times 10^{-11}~\mathrm{m}, which was also known at the time.
\begin{aligned} k &= \frac{\sqrt{-2mE_n}}{\hbar} \\ &= \frac{\sqrt{\frac{m^2e^4}{16 \pi^2 \varepsilon_0^2 n^2 \hbar^2}}}{\hbar} \\ &= \frac{me^2}{4 \pi \varepsilon_0 n \hbar^2} \\ &= \frac{1}{a_0 n}\end{aligned}
And that's enough, more than enough really.
This would not have been possible without the help of my textbook, "An Introduction to Quantum Mechanics" 2nd Edition, by David J. Griffiths (primarily chapter 4). It's a great text book, it helped me heaps in my study (when I actually got around to using, 2 weeks before the exam), was fairly easy to follow, and really interesting.
